Professor Joseph B. Kadane and the Institute of Mathematical Statistics gave their permission to publish this article on our website.

Bayesian Thought in Early Modern Detective Stories:
Monsieur Lecoq, C. Auguste Dupin and Sherlock Holmes

Author: Joseph B. Kadane
Professor of Statistics and Social Sciences, Emeritus
Abstract: This paper reviews the maxims used by three early modern fictional detectives: Monsieur Lecoq, C. Auguste Dupin and Sherlock Holmes. It find similarities between these maxims and Bayesian
thought. Poe’s Dupin uses ideas very similar to Bayesian game theory. Sherlock Holmes’ statements also show thought patterns justifiable in Bayesian terms.
Key words and phrases: Arthur Conan Doyle, Edgar Allan Poe, Emile
Gaboriau, odd and even, Bayesian Game Theory.

BAYESIAN DETECTIVES
1. INTRODUCTION
The three writers considered here, Emile Gaboriau (1832–1873), Edgar Allan Poe (1809–1849) and
Sir Arthur Conan Doyle (1859–1930) are considered
to be the founders of the modern interest in detective stories, writing even before the term “detective”
was used (Bleiler, 1975). In addition to the many
novels and short stories that have ensued, there are
also popular television crime, mystery and police
shows that can be considered progeny. This popularity continues despite the weaknesses in the underlying forensic science, as emphasized by a recent
report of the National Research Council (2009).
This essay aims to examine the pattern of thought
used by their respective detectives: Monsieur Lecoq,
C. Auguste Dupin and Sherlock Holmes. What does
it mean to understand the thoughts of a fictional
character? With a real person, one can ask questions and run experiments to ascertain how they
think. Although indirect methods such as functional
magnetic resonance imaging (fMRI) cannot yet be
used to tell what a person is thinking, it is not impossible that in the future this may be possible. We
have so-called lie-detector machines, although another National Research Council Report (2003) has
seriously challenged their accuracy.
On the other hand, there is a sense in which understanding fictional characters is easier than understanding real ones.
There is a fixed body of written
work, and this is all the evidence there will ever be.
Those words tell what characteristics of the detectives the author considers most important. When
the author writes about the way such characters
go about their work, this can be taken to be authoritative. Thus there is no issue, for example, of
changing or molding the responses that a real person
might give in response to a question framed in a way
the respondent hadn’t considered previously. Thus
we may take the statements written by the authors
as summaries of what they intend their characters
(here, detectives) to teach the readers.

2. EMILE GABORIAU’S MONSIEUR LECOQ
The plot of the novel Monsieur Lecoq (1869) and
its sequel In Honor of the Name Gaboriau (1975) revolves around the efforts of novice detective Lecoq to
establish the identity of a prisoner who killed three
people in a brawl in a bar on the outskirts of Paris.
The intricacies are enormous, and in the end Lecoq
goes to a wise-man consulting detective who essentially solves the case for him.
Little is written about Lecoq’s methods, except
for one refrain that occurs three times: “Always suspect that which seems probable; and begin by believing that which appears incredible” (page 79),
“Distrust all circumstances that seem to favor your
secret wishes” (page 87), and “Always distrust what
seems probable!” (page 248). Taken together they
suggest a tinge of paranoia, perhaps (but what is a
poor detective to do in the hands of a malign author intent on surprising the reader and, one supposes, his own detective?).
It also suggests a touch
of Lindley’s Cromwell’s Rule, not to put zero probability on any conceivable possibility (Lindley, 1985,
page 104).
We can’t go further with Lecoq’s maxims or theories, because Gaboriau doesn’t give us any.

3. EDGAR ALLAN POE’S C. AUGUSTE DUPIN
In The Murders in the Rue Morgue Poe (1944),
Dupin and a friend read newspaper accounts of two
murders in a fourth story room locked from the inside. The mother’s throat was slashed many times;
the daughter was suffocated and her body stuffed
up a chimney. Dupin offers to help the police, and
is given access to the crime scene. He finds hair that
he is sure is not human. (I won’t leave you hanging too long, but first want to introduce you to the
problems in the other two Dupin stories.)
In The Mystery of Marie Rogêt, a young woman’s
body is found floating in the Seine River. Using
newspaper accounts, Dupin challenges much of the
rationale in those stories. The case and the newspaper accounts all did occur in New York City, to
a young woman named Mary Cecilia Rogers. Her
case is still regarded as unsolved, although there are
hints that her death may have been the result of an
unsuccessful abortion.
Finally, The Purloined Letter is the most famous
of the three Dupin stories. A police prefect asks
Dupin’s help in finding and returning a letter concerning a high-placed lady who saw the letter being
taken by Minister D., but was helpless to prevent the
theft. Minister D. has since been using the letter for
blackmail. The prefect states that the letter has not
been revealed, because the consequences that would
have ensued from its release have not occurred. Second, Minister D. must have the letter close at hand
for it to be useful to him. Finally, using various subterfuges, the police have carefully searched all the
hiding places in Minister D.’s rooms, behind the
wallpaper, hidden in a hollow leg of furniture, etc.,
without result. They have also twice found ways to
search Minister D.’s body, again without finding the
letter.

What is important to us in these three stories
is the theory Poe promulgates as to how Dupin is
thinking about the puzzles he sets himself to solve.
In a preamble to The Murders in the Rue Morgue,
Poe writes of his views on skill in games. The first
of these is chess, which he regards as principally a
matter of attention (the loser, by inattention, makes
a blunder). (I don’t think Poe is correct about chess
among decent players, as winners are often those
who employ sound openings, develop their pieces,
pay attention to their pawn structure, protect their
king, fight for control of important center squares,
and gradually accumulate little advantages all the
while thwarting his opponent’s attempts to do the
same to him.) Draughts (now called checkers) interests Poe more. For example, if the game is reduced
to four kings, he writes “Deprived of ordinary resources, the analyst throws himself into the spirit of
his opponent, identifies himself therewith, and not
unfrequently sees thus, at a glance, the sole methods (sometimes absurdly simple ones) by which he
may seduce into error or hurry into miscalculation”
(page 47).
The third game to interest Poe is whist, which is
roughly like bridge without bidding.
. . proficiency in whist implies capacity for
success in all these more important undertakings where mind struggles with mind.
When I say proficiency, I mean that perfection in the game which includes a comprehension of all the sources whence legitimate advantage may be derived. These
are not only manifold, but multiform, and
lie frequently among recesses of thought
altogether inaccessible to the ordinary understanding.
. . . it is in matters beyond the limits of
mere rule that the skill of the analyst is
evinced. He makes, in silence, a host of
observations and inferences. So, perhaps,
do his companions; and the difference in
the extent of the information obtained,
lies not so much in the validity of the inference as in the quality of the observation. The necessary knowledge is that of
what to observe. Our player confines himself not at all; nor, because the game is
the object, does he reject deductions from
things external to the game. He examines the countenance of his partner, comparing it carefully with that of each of
his opponents. He considers the mode of
assorting the cards in each hand; often
counting trump by trump, and honor by
honor, through the glances bestowed by
their holds on each. He notes every variation of face as the lay progresses, gathering a fund of thought from the differences
in the expression of certainty, of surprise,
of triumph, of chagrin. From the manner
of gathering up a trick he judges whether
the person taking it, can make another in
the suit.
The first two or three rounds having been
played, he is in full possession of the contents of each hand, and thenceforward puts
down his cards with as absolute a precision of purpose as if the rest of the party
had turned outward the faces of their own.
The analytical power would not be confounded with simple ingenuity; for while
the analyst is necessarily ingenious, the
ingenious man is often remarkably incapable of analysis.
Between ingenuity and the analytic ability there exists a difference far greater,
indeed, than that between the fancy and
the imagination, but of a character very
strictly analogous. It will be found, in fact,
that the ingenious are always fanciful, and
the truly imaginative never otherwise than
analytic (pages 48, 49).
It is this talent that Dupin is called upon to exemplify. For example, how did the murderer or murderers escape from the murder room in The Murders in
the Rue Morgue? “I knew that all apparent impossibilities must be proved not to be such in reality. I
proceeded to think, thus—a posteriori. The murderers did escape from one of these windows. This being
so, they could not have re-fastened the sashes from
the inside, as they were found to be fastened. . .Yet
the sashes were fastened. They must, then, have the
power of fastening themselves” (pages 72, 73, emphasis in original). Dupin then goes on to show that
while the two windows look the same, one of them
could fasten itself. He thus establishes how the murderers escaped.
Putting together the wild brutality of the murders, the enormous strength it must have taken to
put the dead daughter’s body up the chimney, and
the nonhuman hair he found on the scene, Dupin
concludes that some ape-like animal must have done
these murders. He places an ad asking if someone has
lost an “Ourang-Outang”. When a sailor shows up,
Dupin learns that he had an orangutan which ecaped with the sailor’s shaving razor, murdered the
two women, and escaped.

Murders in the Rue Morgue
by Berni Wrightson
What can we say of how well Dupin’s deductions
used Poe’s theories? Certainly his deduction about
egress is using a combination of Bayes’ rule and
Lindley’s “Cromwell’s Rule.” However, perhaps we
can excuse this omission of the use of his ideas about
game theory in the light of the bouquet Poe throws
to all the readers of this journal:
Coincidences, in general, are great stumbling-blocks in the way of that class of
thinkers who have been educated to know
nothing of the theory of probabilities
that theory to which the most glorious of
human research are indebted for the most
glorious of illustration (page 77).
As already mentioned, The Mystery of Marie Rogêt,
remains a mystery. Solving real cases is no doubt
more demanding than solving fictional ones. Nonetheless, there is one passage that demands our attention. Poe writes,
[The journal L’Etoile writes] ‘All experience has shown that drowned bodies, or
bodies thrown into the water immediately
after death by violence, require from six
to ten days for sufficient decomposition to
take place to bring them to the top of the
water.’
These assertions have been tacitly received
by every paper in Paris, with the exception of Le Moniteur.1 This latter print endeavors to combat that portion of the paragraph which has reference to ‘drowned
bodies’ only, by citing some five or six instances in which the bodies of individuals
known to be drowned were found floating after the lapse of less time than is insisted upon by L’Etoile. But there is something excessively unphilosophical in the
attempt, on the part of Le Moniteur, to rebut the general assertion of L’Etoile, by a
citation of particular instances militating
against that assertion. Had it been possible to adduce fifty instead of five examples
of bodies found floating at the end of two
or three days, these fifty examples could
still have been properly regarded only as
exceptions to L’Etoile’s rule, until such
time as the rule itself should be confuted.
Admitting the rule (and this Le Moniteur
does not deny, insisting merely upon its
exceptions), the argument of L’Etoile is
suffered to remain in full force; for this argument does not pretend to involve more
than a question of the probability of the
body having risen to the surface in less
than three days; and this probability will
be in favor of L’Etoile’s position until the
instances so childishly adduced shall be
sufficient in number to establish an antagonistical rule (pages 112, 113).
This is an important and subtle point, one that
it took the medical profession another century to
incorporate, via the use of controlled clinical trials.
Finally, we come to Poe’s masterpiece, The Purloined Letter. Dupin further expands on the theory
he is using in solving the case by discussing yet another game, as follows:
I knew one [school-boy] about eight years
of age, whose success at guessing in the
game of ‘even and odd’ attracted universal admiration. This game is simple, and
is played with marbles. One player holds
in his hand a number of these toys and
demands of another whether that number
is even or odd. If the guess is right, the
guesser wins one; if wrong, he loses one.
The boy to whom I allude won all the
marbles of the school. Of course he had
some principle of guessing; and this lay
in mere observation and admeasurement
of the astuteness of his opponents. For
example, an arrant simpleton is his opponent, and, holding up his closed hand,
asks, ‘Are they even or odd?’ Our school-
boy replies, ‘Odd,’ and loses; but upon the
second trial he wins, for he then says to
himself: “The simpleton had them even
upon the first trial, and his amount of cunning is just sufficient to make him have
them odd upon the second; I will therefore
guess odd’;—he guesses odd, and wins.
Now, with a simpleton a degree above the
first, he would have reasoned thus: ‘This
fellow finds that in the first instance I guessed
odd, and, in the second, he will propose to
himself, upon the first impulse, a simple
variation from even to odd, as did the first
simpleton; but then a second thought will
suggest that this is too simple a variation,
and finally he will decide upon putting
it even as before. I will therefore guess
even’;—he guesses even, and wins. Now
this mode of reasoning in the school-boy,
whom his fellows termed ‘lucky,’—what,
in its last analysis, is it?
‘It is merely,’ I said, ‘an identification of
the reasoner’s intellect with that of his opponent’ (pages 165, 166).
If we identify utilities with marbles, this is a zerosum two person game. The minimax strategy, independently one-half probability on odds and half on
evens, seems a very poor recommendation to this
young genius.
Dupin reasons as follows: Minister D. knows the
methods of the police. They are extremely good at
ferreting out and exploring all of the hidden places
the letter might be. None of those searchers has succeeded. Thus Minister D., knowing what he does
about the police, does not put it in any of these
places. Where then? It must be in plain sight!
To test his idea, Dupin visits Minister D., wearing
eyeglasses that obscure where his eyes are focusing.
He sees a scruffy document hanging, observes that
it is folded inside out, and deduces that this must
be the letter. Leaving a gold snuff box so he has
an excuse to return the next day, Dupin has a document prepared that matches the new exterior of
the letter. Returning the next day, purportedly to
pick up his snuff box, a cannon goes off in the street
below (which Dupin had arranged). Minister D. is
distracted, Dupin switches his fake for the real letter, and leaves with both the real letter and his gold
snuff box.
In this story, Poe has finally delivered on his promise.
Dupin has used his understanding of Minister D.’s
thought process to identify where the letter is. The
Purloined Letter is a wonderful story. It enchanted
me as a child, and still does.


4. SIR ARTHUR CONAN DOYLE’S
SHERLOCK HOLMES
We do not need to speculate about the antecedents
Doyle had in mind. In his autobiography, Memories
and Adventures Doyle (1924) he writes:
" Gaboriau had rather attracted me by the
neat dovetailing of his plots, and Poe’s
masterful detective, M. Dupin, had from
boyhood been one of my heroes. But could
I bring an addition of my own? I thought
of my old teacher Joe Bell, . . . of his eerie
trick of spotting details. If he were a detective, he would surely reduce this fascinating but unorganized business to something nearer an exact science. " (page 69)
In contrast to Gaboriau’s single (or perhaps double) book and Poe’s three short stories, Doyle (1981)
gives us four Sherlock Holmes novels and 56 short
stories. So we have in one sense a great deal of information. However, Doyle seems less anxious than
Poe to show us how Holmes is thinking about his
tasks. When he does so, on occasion those thoughts
are often reminiscent of ideas already in Poe’s stories. For example, in The Adventure of the Second
Stain from The Return of Sherlock Holmes, a letter
from a foreign power has been stolen. If its content
were known, it could cause various foreign upsets.
“Only one important thing has happened in the last
three days, and that is that nothing has happened”
(page 659). It seems to me that this is much like the
evidence in The Purloined Letter that the letter had
not been used.
Similarly, in The Hound of the Baskervilles,
Holmes says “If . . .we are dealing with forces outside
the ordinary laws of Nature, there is an end to our
investigation. But we are bound to exhaust all other
hypotheses before falling back upon this one” (page
684). I find this reasoning similar to that Dupin used
in ascertaining how the murderer(s) left the scene of
the murders in Murders in the Rue Morgue.
There is one passage, in the conclusion to A Study
in Scarlet, where I think Doyle is aiming to clarify what Poe is trying to get at on the subject of
analytic reasoning: “Most people, if you describe a
train of events to them, will tell you what the result
would be. They can put those events together in
their minds, and argue from them that something
will come to pass. There are few people, however,
who, if you told them a result, would be able to
evolve from their own inner consciousness what the
steps were that led to that result. This power is what
I mean when I talk of reasoning backward, or analytically” (pages 83, 84). So Doyle (Holmes) is saying
that predicting subsequent from preceding events is
relatively straightforward, but the reverse is hard.
And this is exactly what Bayes’ Theorem does.
However, that theorem is even more evident in
what we must take as Holmes’ slogan, as it is repeated four times in the work (pages 111, 315, 926,
1011). “When you have eliminated the impossible,
whatever remains, however unlikely, must be the
truth.”
This is formulated sufficiently crisply that it can
actually be proved as follows: Let H1, . . . ,Hk be k
theories of the case, mutually exclusive (not more
than one can be true), exhaustive (one of them must
be true), and suppose each has positive prior probability. In fact, we’ll think of H1 as the theory (how-
ever unlikely) that is not eliminated by the data.
Suppose we have data X that has eliminated theories H2, . . . ,Hk, that is,
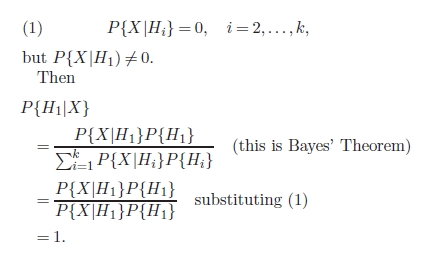
Thus no matter how small P{H1} may have been,
the posterior probability of H1 under these circumstances is one.
Thus Sherlock Holmes is using, and insisting upon,
Bayesian results to explain his actions.

5. CONCLUSION
To make this conclusion maximally embarrassing
(and hence possibly entertaining to the reader), I present
it as if I were being cross-examined by C:
C: Dr. Kadane, is it correct that you are familiar
with Bayes’ Theorem?
K: Yes.
C: How would you describe Sherlock Holmes’ use of
Bayesian ideas?
K: Holmes certainly seems to understand the ideas,
and how to use them.
C: Is it known whether Doyle had an acquaintance
with mathematics sufficient that he might be familiar with a mathematical version of the theorem?
K: It is known that Doyle was trained and qualified
as a physician. I do not know the extent to which
some math may have been part of that training.
Therefore my answer to your question is “I don’t
know.”
C: Very well, whether or not Doyle had that mathematical training, does Holmes, in Doyle’s hands,
correctly use Bayes’ Theorem?
K: Yes, I think he does.
C: Does he make any errors he might have avoided
had Doyle had a more mathematical grasp of
Bayes’ Theorem?
K: None that I have found.
C: Very well, now let’s turn to Poe’s work. Dr. Kadane,
do I understand correctly that you have written a paper about the connection between games
and Bayesian theory?
K: Yes, Pat Larkey and I wrote a paper entitled
“Subjective Probability and the Theory of Games”
(Kadane and Larkey, 1982).
C: Would you tell us briefly the main argument of
that paper?
K: Surely. The idea is that if I am playing a game
against you, my main source of uncertainty is
what you will do. As a Bayesian I have probabilities on what you will do, and can use them to
calculate my maximum expected utility choice,
which is what I should choose.
C: Is this consistent with what Poe writes about
games?
K: Very much so. The marble king of Poe’s acquaintance is very good at guessing his opponent’s
strategy, which is how he winds up with all the
marbles in his school. Dupin is successful at understanding Minister D.’s strategy, and hence in
finding and retrieving the letter.
C: Is there anything that Poe writes about games
that is inconsistent with your theory?
K: No.
C: On the other hand, is there anything in your
paper that would have helped Poe had it been
available more than a century before it was?
K: Nothing I can think of.
C: Now, is it also the case that you have written on
the subject of skill in games, is that correct?
K: Yes. Four of us, the others were Pat Larkey again,
Robert Austin and Shmuel Zamir, wrote a paper
by that title, published in Operations Research
(Larkey et al., 1997).
C: Again, briefly, what is this paper about?
K: We create a simplified version of poker, and simulate contests among various strategies for playing the game. One interesting finding was non-
transitivity: under certain circumstances, there
could be strategies A, B and C, where A is effective against B, B against C and C against A.
So there isn’t among these, a “best” strategy at
all.
C: Is there anything in this paper that would have
deepened Poe’s understanding of skill in games?
K: I don’t think so. I think Poe understood skill
in games very well, both in how Dupin outwits
Minister D., and in his general introduction. As
I explained earlier, I disagree with him about
chess, but as a general matter, his view of skill
in games is very similar to the one in our papers.
C: So then is it your thought that you have very
little news for either Doyle or Poe?
K: Yes, I think that is fair.
C: Then what has been going on in this field for the
last 100 or 150 years? Have we gotten nowhere?
K: I don’t think that is a fair characterization. What
is new is that through the work of Ramsey (1926),
de Finetti (1970, 1975), Savage (1954), DeGroot
(1970) and Lindley (1985), we now have a general theory of what it means to make good decisions in the face of uncertainty. That theory
rests on a few simple principles:
– all sources of uncertainty are modeled probabilistically,
– as data became available, the probability models are updated by conditioning on the observed data,
– when it is required that decisions be made, the
optimal decision maximizes expected utility,
where the expectation is taken with respect to
the current (updated) opinion of the decision
maker.
Thus we now understand both Bayes’ Theorem
and the Bayesian approach to games as special
cases of this very general theory. That’s what’s
new.
C: Thank you, Dr. Kadane.
Both detective stories and Bayesian analysis have
flourished in the intervening century. They share
some common roots.

Bayesian Thought in Early Modern Detective Stories:
Monsieur Lecoq, C. Auguste Dupin and Sherlock Holmes

Institute of Mathematical Statistics site:
imstat.org
REFERENCES
Bleiler, E. (1975). Introduction to the Dover Edition of Gaboriau’s Monsiur Lecoq. Dover, New York.
De Finetti, B. (1970, 1975). Theory of Probability. Wiley,
Chichester. (Translated by A. Machi and A. F. M. Smith.)
MR0440641
DeGroot, M. (1970). Optimal Statistical Decision. McGraw
Hill, New York. MR0356303
Doyle, A. C. (1924). Memories and Adventures. Little
Brown & Co., Boston.
Doyle, A. C. (1981). The Penquin Complete Sherlock
Holmes. Viking Penguin, New York.
Gaboriau, E. (1975). Monsieur Lecoq. Dover Publications,
New York.
Kadane, J. and Larkey, P. (1982). Subjective probability
and the theory of games. Management Sci. 28 113–120.
MR0652016
Larkey, P., Kadane, J., Austin, R. and Zamir, S. (1997).
Skill in games. Management Sci. 43 596–609.
Lindley, D. (1985). Making Decisions. Wiley, Chichester.
MR0892099
National Research Council (2003). The polygraph and
lie detection. National Academies Press, Washington, DC.
National Research Council (2009). Strengthening forensic science in the United States: A Path Forward. National
Academies Press, Washington, DC.
Poe, E. (1944). Tales of Edgar Allan Poe. Random House,
New York.
Ramsey, F. (1926). Truth and probability. In Studies in
Subjective Probability (H. E. Kyburg and H. E. Smokler,
eds.) RE Kreiger Publishing (Reprinted). Huntington, NY.
MR0584256
Savage, L. (1954). The Foundations of Statistics. Wiley, New
York. MR0063582
Professor Joseph Born Kadane and the Institute of Mathematical Statistics gave their permission to publish this article on our website.
Sherlockian-sherlock.com
|












